3.5. Example: Silver and Copper Clusters
Tip
The sample input and output files can be found in testfiles/atom/3-agcu.
3.5.1. Ag38 and Cu38
The systems here are two metallic clusters: \(\mathrm{Ag}_{38}\) and \(\mathrm{Cu}_{38}\). The interactions are modelled by Gupta potential. The parameters can be found in misc/atomic-force-field.txt:
Cu-Cu 0.0855 1.224 2.556 10.96 2.278 # Phys. Rev. B 48, 22, 1993
Cu-Au 0.1539 1.5605 2.556 11.05 3.0475 # Phys. Rev. B 48, 22, 1993
Cu-Ag 0.0980 1.2274 2.7224 10.700 2.8050 # J. Chem. Phys. 2011, 135, 164109
Au-Au 0.2061 1.79 2.884 10.229 4.036 # Phys. Rev. B 48, 22, 1993
Ni-Ni 0.038 1.07 2.491 16.999 1.189 # Phys. Rev. B 48, 22, 1993
Rh-Rh 0.0629 1.66 2.69 18.45 1.867 # Phys. Rev. B 1993, 48, 22
Ag-Ag 0.1028 1.178 2.88 10.928 3.139 # Phys. Rev. B 1993, 48, 22
Ir-Ir 0.1156 2.289 2.72 16.98 2.691 # Phys. Rev. B 1993, 48, 22
Attention
As mentioned in Theoretical Background, Gupta potential is not suitable for small metallic clusters. Here we just want to demonstrate the function of atom.
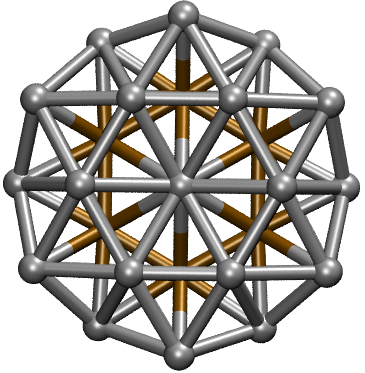
Consider \(\mathrm{Ag}_{38}\) first.
Step 1: call abcinp to generate input files:
$ abcinp Ag38 1 Gupta 10 100 100 5 20 38 Ag
Parameters for atom-pair 0-0: A xi d p q > 0.1028 1.1780 2.8885 10.928 3.1390
Step 2: Run the global optimization:
$ atom Ag38.inp > Ag38.out
After a few seconds, you will find the global minimum in Ag38.xyz (see below) and local minima in Ag38-LM.
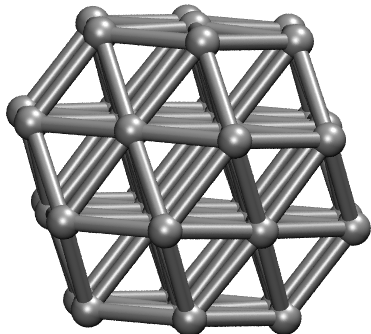
For \(\mathrm{Cu}_{38}\), the global optimization is similar.
Tip
You can try to search \(\mathrm{Zn}_{38}\). Its global minimum has a completely different geometry from \(\mathrm{Ag}_{38}\) and \(\mathrm{Cu}_{38}\).
3.5.2. Ag32Cu6
Now we consider a mixed metallic clusters: \(\mathrm{Ag}_{32}\mathrm{Cu}_{6}\). Will it have a similar global minimum with \(\mathrm{Ag}_{38}\) and \(\mathrm{Cu}_{38}\)?
Step 1: call abcinp to generate input files:
$ abcinp Ag32Cu6 2 Gupta 10 3000 100 5 20 32 Ag 6 Cu
Parameters for atom-pair 0-0: A xi d p q > 0.1028 1.1780 2.8885 10.928 3.1390
Parameters for atom-pair 0-1: A xi d p q > 0.0980 1.2274 2.7224 10.700 2.8050
Parameters for atom-pair 1-1: A xi d p q > 0.0855 1.2240 2.5562 10.960 2.2780
Note that the population size 3000 and number of generations 100 are quite large, since this system is a difficult one for global optimization.
Step 2: Run the global optimization:
$ atom Ag32Cu6.inp > Ag32Cu6.out
After a few seconds, you will find the global minimum in Ag32Cu6.xyz (see below) and local minima in Ag32Cu6-LM. Unlike the face-centred-cubic truncated octahedron cluster of \(\mathrm{Ag}_{38}\), this global minimum has somewhat unexpected D 6h symmetry.