6.5. geom with xTB

As discussed in isomer with xTB, xTB is highly recommended for global optimization of chemical clusters that are unable to be described by force fields.

There are two ways of calling xTB in geom:

• Use misc/runxTB.sh as discussed in isomer with xTB, just like

geom.inp

commands
    ./runxTB.sh $inp$ $out$ $xxx$
end

To use this way, you must have an extra xTB installed on your system.

• Use $xTB$ as discussed in Input File for geom.

geom.inp

xtb
    0 0 2
end
commands
    $xTB$
end

The advantage of this way is that you do NOT have to install xTB because these computation subroutines are already available internally in geom!

As discussed in Input File for geom, the three integers in xtb block are:

• the charge of the whole cluster,

• the number of unpaired electrons,

• the Hamiltonian type (0, 1, 2, or 3 (means GFN-FF)).

Tip

For atomic clusters, the Hamiltonian type is recommended to be set to 1. For other cases, 0, 1, and 2 are all good. For large organic or organometallic compounds, 3 may also be a good choice.

6.5.1. Example: NaCl(H2O)10

Tip

The sample input and output files can be found in testfiles/geom/4-naclh2o10-xTB.

In this Section we will see how to use geom to look for the global minimum of \(\text{NaCl}(\text{H}_2\text{O})_{10}\).

The structures of the 3 species are:

h2o.xyz

3
water
O                  0.00000000    0.00000000   -0.11081188
H                  0.00000000   -0.78397589    0.44324751
H                 -0.00000000    0.78397589    0.44324751

na.xyz

1
Na
Na  0 0 0

cl.xyz

1
Cl
Cl  0 0 0

The input file is:

naclh2o10.inp

lm_dir          naclh2o10 # Save the local minima to this folder.
num_calcs       2000     # Total number of calculations.
do_coarse_opt   yes      # no: Do NOT the coarse optimization.
min_energy_gap  1.E-4    # When two energies differ smaller than
                         # this value, they are treated as identical.
                         # A negative number means do not remove
                         # energetically degenerated ones.
max_geom_iters  3000     # The maximum number of iterations for local optimization.
                         # If it is less or equal than zero, then the number is unlimited.

components
    h2o.xyz 10
    random 0 0 0 8 8 8
    ****
    na.xyz 1
    random 0 0 0 8 8 8
    ****
    cl.xyz 1
    random 0 0 0 8 8 8
    ****
end

xtb
 0 0 1
end

commands
   $xTB$
end

You can see that, we let all molecules distribute randomly in a box defined by (0, 0, 0) and (8, 8, 8).

Now you can run the global optimization:

$ geom naclh2o10.inp > naclh2o10.out

After the optimization, the end of naclh2o10.out is

naclh2o10.out

 -- Result Report --
Results are energy-increasingly reordered.
Structures of energies within 1.000E-04 are treated as degenerate.
All minima are saved to "naclh2o10".
-------------------------------------------------------------------
     #  index               Energy            NaiveRMSD
-------------------------------------------------------------------
     0    410         -78.90900677           0.00000000
     1   1315         -73.85642855          11.13424019
     2    270         -72.33437367           8.23789070
     3    471         -71.89726049           2.84818350
     4    595         -71.66037145           0.96099577
     5   1138         -71.33515351           1.70326738
     6    656         -71.30962706           6.91732743
     7    309         -70.21312469           8.33181645
     8   1007         -69.27883414           4.11576652
     9    424         -68.96145859           1.36910299
    10    777         -68.61390125           9.25461485
     ... omitted ...
    28    966         -63.05453856          10.34934592
    29    863         -62.49368470           9.79444040
    30   1883         -62.49337541           9.23302757
    31    648         -62.49194643           9.39246214
    32   1811         -62.49123647           9.68901769
    33    859         -62.49102429           9.53495472

Here you must be cautious. The lowest 29 structures, i.e. naclh2o10/410.xyz, naclh2o10/1315.xyz, … naclh2o10/966.xyz are highly dispersed, distorted unreasonable structures (see below), but they have uncommonly low energies. These misleading energies may occur when the initial guess is far away from equilibrium structures and often result from un-converged SCF processes.

After checking the energies, it seems that energies higher than -63 are normal ones. Indeed, the global minimum of this system is naclh2o10/863.xyz, which is shown below:

Tip

In practice, to further refine structures, like naclh2o10\863.xyz and naclh2o10/1883.xyz, you can use Gaussian or ORCA to do more accurate optimization.

6.5.2. Example: Co6Te8(PEt3)6

Tip

The sample input and output files can be found in testfiles/geom/5-co6te8pet36-xTB.

In this Section we will consider a quantum dot \(\text{Co}_6\text{Te}_8(\text{PEt}_3)_6\). It has a \(\text{Co}_6\text{Te}_8\) core ligated with 6 \(\text{PEt}_3\). Since we have no idea of its structure at this moment, we will search the core first.

6.5.2.1. Co6Te8

We can use exactly the same way as we have done for \(\text{NaCl}(\text{H}_2\text{O})_{10}\).

The structures of the 2 species are:

co.xyz

1
Co
Co  0 0 0

te.xyz

1
Te
Te  0 0 0

The input file is:

co6te8.inp

lm_dir          co6te8   # Save the local minima to this folder.
num_calcs       2000     # Total number of calculations.
do_coarse_opt   yes      # no: Do NOT the coarse optimization.
min_energy_gap  1.E-4    # When two energies differ smaller than
                         # this value, they are treated as identical.
                         # A negative number means do not remove
                         # energetically degenerated ones.
max_geom_iters  3000     # The maximum number of iterations for local optimization.
                         # If it is less or equal than zero, then the number is unlimited.

components
    co.xyz 6
    random 0 0 0 8 8 8
    ****
    te.xyz 8
    random 0 0 0 8 8 8
    ****
end

xtb
 0 0 1
end

commands
   $xTB$
end

Now you can run the global optimization:

$ geom co6te8.inp > co6te8.out

After the optimization, the end of co6te8.out is

co6te8.out

 -- Result Report --
Results are energy-increasingly reordered.
Structures of energies within 1.000E-04 are treated as degenerate.
All minima are saved to "co6te8".
-------------------------------------------------------------------
     #  index               Energy            NaiveRMSD
-------------------------------------------------------------------
     0    954     -255485.30137014           0.00000000
     1   1649      -13270.21996894           9.77918423
     2    708        -379.80860329           8.25823482
     ... omitted ...
   108    929         -51.90294094           9.92663264
   109     29         -51.86444358           8.63886023
   110     66         -51.86429930           9.29717029
   111    199         -51.84758402           9.00426358
   112   1213         -51.84370999           9.19951625

After checking the energies, reasonable ones should be higher than about -51.8. Thus, the global minimum should be co6te8/29.xyz, which is shown below.

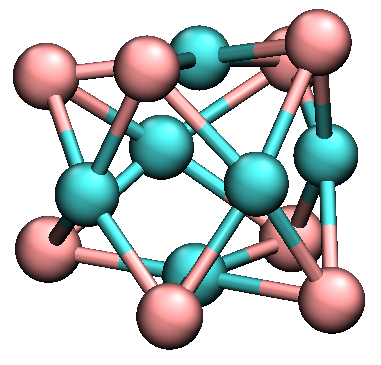
6.5.2.2. Co6Te8(PEt3)6

Now we will consider the ligation of \(\text{PEt}_3\), whose structure is:

pet3.xyz

 22
PEt3
 P                  0.77411167    0.93908628    0.00000000
 C                  1.38078883    1.79703460   -1.48602405
 H                  1.02413441    2.80584461   -1.48602405
 H                  2.45078883    1.79702166   -1.48602419
 C                  0.86744661    1.07107703   -2.74342827
 H                  1.19588317    1.59486033   -3.61674408
 H                  1.25178947    0.07263744   -2.76071851
 H                 -0.20200553    1.04133445   -2.72647284
 C                  1.58017719   -0.68723832    0.13314147
 H                  1.06926441   -1.39066966   -0.49059924
 H                  2.59983880   -0.60671904   -0.18103498
 C                  1.53001448   -1.16683089    1.59569905
 H                  1.95386617   -2.14689639    1.66441129
 H                  2.08820972   -0.49286368    2.21139887
 H                  0.51311419   -1.19395588    1.92747918
 C                  1.16337141    1.93168334    1.47500099
 H                  0.62390995    1.54801668    2.31564434
 H                  0.88119749    2.94963161    1.30453342
 C                  2.67528550    1.85868155    1.75852616
 H                  3.05363867    2.84440501    1.93201431
 H                  2.84706388    1.25327881    2.62390451
 H                  3.17563928    1.42763883    0.91665428

For the core, we will just use the global minimum co6te8/29.xyz, which is renamed to co6te8.xyz and shown below:

co6te8.xyz

14
-51.86444358
Co           5.18912366           4.53807660           5.15436968
Co           4.63921329           6.73032694           4.33024999
Co           5.57653575           4.28771551           2.73430585
Co           3.73287281           2.69503667           3.34312049
Co           3.09922668           5.44745620           2.69377997
Co           2.32298551           4.63312799           4.83935341
Te           3.65939955           5.91817891           6.45016152
Te           5.16439545           6.53843136           1.92985727
Te           1.55874524           3.57414579           2.71643092
Te           3.68082433           2.75955616           5.79296888
Te           5.94894157           2.39529023           4.27916498
Te           2.22874466           7.03012888           4.38569672
Te           3.80790879           3.72603676           1.12877717
Te           6.88875884           5.89174763           3.98837449

The input file is:

co6te8pet36.inp

lm_dir          co6te8pet36   # Save the local minima to this folder.
num_calcs       200       # Total number of calculations.
do_coarse_opt   yes      # no: Do NOT the coarse optimization.
min_energy_gap  1.E-4    # When two energies differ smaller than
                         # this value, they are treated as identical.
                         # A negative number means do not remove
                         # energetically degenerated ones.
max_geom_iters  3000     # The maximum number of iterations for local optimization.
                         # If it is less or equal than zero, then the number is unlimited.

components
    co6te8.xyz 1
    fix 0 0 0 0 0 0
    ****
    pet3.xyz 6
    shell 1 1 1 2 9 16 0 0 0 4 4 4
    ****
end

xtb
 0 0 1
end

commands
   $xTB$
end

From components, we can see that the core \(\text{Co}_6\text{Te}_8\) is fixed at (0, 0, 0) without rotation. Since its diameter is about 6 Å, we let the 6 \(\text{PEt}_{3}\) form a shell on an ellipsoid centered at (0, 0, 0) with radii 4, 4, and 4. They point to the shell with an axis defined by the average of atom 1, 1, 1 and 2, 9, 16.

Now you can run the global optimization:

$ geom co6te8pet36.inp > co6te8pet36.out

After the optimization, the end of co6te8pet36.out is

co6te8pet36.out

 -- Result Report --
Results are energy-increasingly reordered.
Structures of energies within 1.000E-04 are treated as degenerate.
All minima are saved to "co6te8pet36".
-------------------------------------------------------------------
     #  index               Energy            NaiveRMSD
-------------------------------------------------------------------
     0      5        -192.73555542           0.00000000
     1     69        -192.73510648           5.73710764
     2     87        -192.73423439           5.54349689
     3    107        -192.73409359           4.88639799
     4    197        -192.73377634           5.63049822
     5    136        -192.73339919           5.57130216
     6     89        -192.73317855           5.26383292

So the global minimum is co6te8pet36/5.xyz, which is shown below.