5.1. isomer with Gaussian

Gaussian is one of the most popular quantum chemistry software, thus we have provided official support for it.

5.1.1. Configuration of Gaussian

If you already know how to configure Gaussian, you can skip this part.

For Windows users: Assume you use Gaussian16 and put it in the directory D:\G16W, then right-click This PC and click Properties, Advanced System Settings, and Environment Variables. In System variables, select PATH and click Edit. In the editbox, add ;D:\G16W at the end of the texts in it, and click OK to confirm it.

For Linux users: Assume you use Gaussian16 and put it in the directory /home/you/g16 and you want to set the scratch directory for calculations to /scratch/you, then open your .bashrc and at the end of the file, add the statements

.bashrc

export g16root="/home/you/g16"
export GAUSS_SCRDIR=/scratch/you
source $g16root/g16/bsd/g16.profile

5.1.2. Example: Al3O4(+)

Tip

The sample input and output files can be found in testfiles/isomer/1-al3o4-g16.

Here we want to find the global minimum of \(\mathrm{Al}_3\mathrm{O}_4^{+}\) at B3LYP/6-31g(d) level of theory. We will show how to use Gaussian and isomer to do this.

Step 1: Prepare an input file named al3o4.inp. For Linux users, use the following content:

al3o4.inp

al3o4         # Result file name
Al 3 O 4      # Symbols
cube 3 3 3    # Structure types
40            # Maximal number of calculations
>>>>
xyz2gaussian optfile $inp$ > $xxx$.gjf
g16 < $xxx$.gjf > $xxx$.log 2>/dev/null
gaussian2xyz $xxx$.log > $out$
>>>>

The texts after # are comments and can be arbitrary. I will explain the input line by line:

The folder name to save local minima.
The cluster components. For \(\mathrm{Al}_3\mathrm{O}_4^{+}\), just write Al 3 O 4.
In this line, one can give the type of initial guesses. Available choices are shown below:

Key words	Meaning
`line`	Generate a linear initial structure.
`plane 2 3`	Generate a plane initial structure from a 2×3 lattice.
`cube 3 4 3`	Generate an initial structure from a 3×4×3 lattice.
Point group symmetry.	Generate a cluster with specific point group symmetry Please see Clusters with Specific Point Group Symmetry for details.

In this case, cube 3 3 3 has 3×3×3 = 27 lattice points. To generate an initial guess, isomer will place 7 atoms (3 aluminum and 4 oxygen atoms) among the 27 lattice points. Thus, the lattice size must be greater than the total number of atoms in the cluster.

Tip

The lattice size should be a little greater than the total number of atoms in the cluster. For example, you want to study a 11-atom cluster \(\mathrm{La}\mathrm{Si}_{10}^{+}\), you should use a guess like cube 4 4 4 (4×4×4=64) but not cube 5 5 5 (5×5×5=125)

The maximum cycle number \(g_{\mathrm{max}}\). Here it is the number of calculations you want to do. See Theoretical Background for details.
The lines between two >>>> are the commands to call external programs. See Interfaces to External Programs for details.

Step 2: Create a file called optfile with the following content:

optfile

%nproc=48
%mem=24GB
#N B3LYP/6-31g(d) SCF(XQC) Geom(NoCrowd) Opt

opt

+1 1
>>>>
>>>>

This is a template file that tells xyz2gaussian how to generate a Gaussian file. Briefly, xyz2gaussian will put all things before the first >>>> to the beginning of the Gaussian input, and all things between the two >>>> after the coordinates in the Gaussian input.

Tip

You should change the number of cores, memory usage, charge, spin multiplicity and # line according to your systems.

Step 3: Now you can run the global optimization:

$ isomer al3o4.inp > al3o4.out

This will take a while (3 hours for me). After the optimization, the end of al3o4.out is

al3o4.out

Reordered from low to high energy:
===============================================================
     #          Energy      Match-RMSD
===============================================================
-1028.18355496      0.00000000
-1028.07587708      1.17242448
-1028.04827707      1.37687293
-1028.04583450      1.42104118
-1028.04460563      1.60199116
-1028.03167498      0.92850705
-1028.02937072      0.96190938
-1028.02418981      1.28093256
-1028.02270757      1.24132082
-1028.01698825      0.83752662
-1028.01572644      0.94141639
-1028.01527907      0.83000691
-1028.01189880      1.08154055

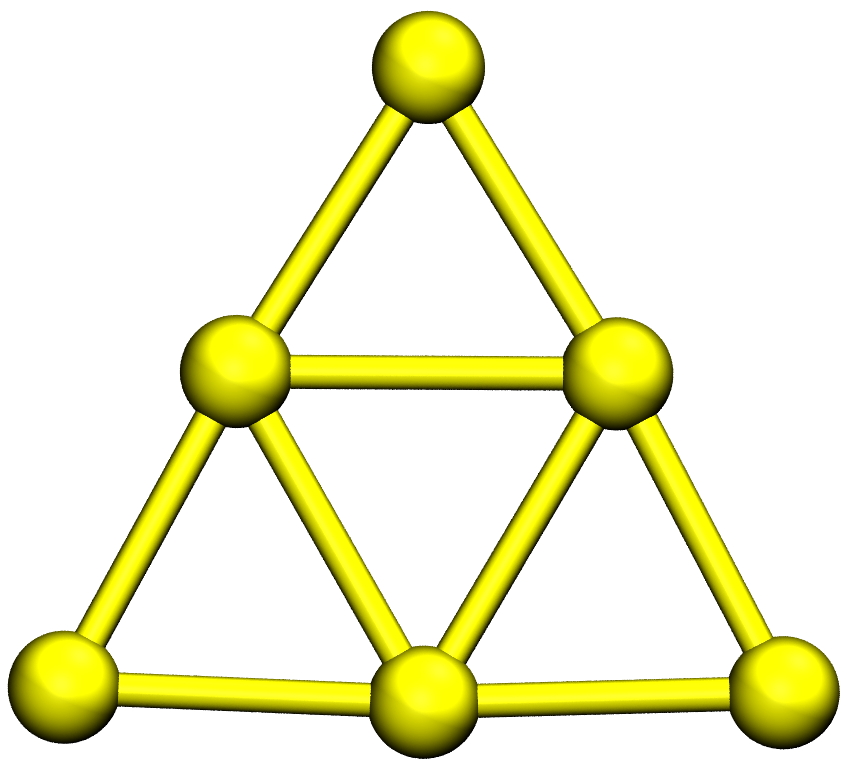
So the global minimum is al3o4-LM/19.xyz and is shown below:

5.1.3. Example: Au6

Tip

The sample input and output files can be found in testfiles/isomer/2-au6-g16.

Here we want to find the global minimum of \(\mathrm{Au}_6\). Assume you have known from literature that the global minima of small gold clusters are flat due to the relativistic effects, we can directly search the global minimum by using plane.

Step 1: Prepare an input file named au6.inp. For Linux users, use the following content:

au6.inp

au6           # Result file name
Au 6          # Symbols
plane 4 3     # Structure types
20            # Maximal number of calculations
>>>>
xyz2gaussian optfile $inp$ > $xxx$.gjf
g16 < $xxx$.gjf > $xxx$.log 2>/dev/null
gaussian2xyz $xxx$.log > $out$
>>>>

In this case, plane 4 3 has 4×3 = 12 lattice points. To generate an initial guess, isomer will place 6 atoms (6 goldatoms) among the 12 lattice points. You can use plane 4 4 if your have plenty of calculation resource. plane 3 3 is too small and is not recommended.

Step 2: Create a file called optfile. For gold, we want to use TPSS functional and a self-defined basis set plus pseudopotential. Remember to put basis information between the two >>>>.

optfile

%nproc=48
%mem=24GB
#N TPSSTPSS/GENECP SCF(XQC) Geom (NoCrowd) Opt

opt

0 1
>>>>
Au 0
S 8 1.00
0.38000800E+02 0.20009000E-01
0.23972500E+02 -0.15167900E+00
0.15218200E+02 0.36396000E+00
0.55399900E+01 -0.82132600E+00
0.13855100E+01 0.93664100E+00
0.64246100E+00 0.42352700E+00
0.15649600E+00 0.16250000E-01
0.54910000E-01 -0.97800000E-03
S 8 1.00
0.38000800E+02 -0.53040000E-02
0.23972500E+02 0.46318000E-01
0.15218200E+02 -0.11994000E+00
0.55399900E+01 0.30406200E+00
0.13855100E+01 -0.49450100E+00
0.64246100E+00 -0.25551600E+00
0.15649600E+00 0.60916300E+00
0.54910000E-01 0.59776700E+00
S 8 1.00
0.38000800E+02 0.32340000E-01
0.23972500E+02 -0.17176200E+00
0.15218200E+02 0.33950300E+00
0.55399900E+01 -0.74617900E+00
0.13855100E+01 0.19174980E+01
0.64246100E+00 -0.11299310E+01
0.15649600E+00 -0.13662840E+01
0.54910000E-01 0.14423910E+01
S 1 1.00
0.54910000E-01 0.10000000E+01
P 7 1.00
0.10309200E+02 0.12821700E+00
0.66276500E+01 -0.35379000E+00
0.16744700E+01 0.56621100E+00
0.80111600E+00 0.49317100E+00
0.34687900E+00 0.11377500E+00
0.12270100E+00 0.25340000E-02
0.42428000E-01 0.67900000E-03
P 7 1.00
0.10309200E+02 -0.35885000E-01
0.66276500E+01 0.10289000E+00
0.16744700E+01 -0.20098800E+00
0.80111600E+00 -0.20104500E+00
0.34687900E+00 0.11654900E+00
0.12270100E+00 0.59496900E+00
0.42428000E-01 0.45552000E+00
P 7 1.00
0.10309200E+02 -0.77242000E-01
0.66276500E+01 0.22261100E+00
0.16744700E+01 -0.49535300E+00
0.80111600E+00 -0.36074700E+00
0.34687900E+00 0.71000000E+00
0.12270100E+00 0.56883900E+00
0.42428000E-01 0.11930000E-02
P 1 1.00
0.42428000E-01 0.10000000E+01
D 6 1.00
0.11002700E+02 0.16467000E-01
0.68916600E+01 -0.68013000E-01
0.18080800E+01 0.29949200E+00
0.82105100E+00 0.45430300E+00
0.34416100E+00 0.34422400E+00
0.12974300E+00 0.12125600E+00
D 6 1.00
0.11002700E+02 -0.23628000E-01
0.68916600E+01 0.95672000E-01
0.18080800E+01 -0.54129400E+00
0.82105100E+00 -0.39553300E+00
0.34416100E+00 0.61916500E+00
0.12974300E+00 0.46827600E+00
D 1 1.00
0.12974300E+00 0.10000000E+01
F 1 1.00
0.89190000E+00 0.10000000E+01
****

Au 0
ECP60MDF 5 60
H-Komponente
1
2 1.000000 0.000000
S-H
2
2 13.523218 426.641867
2 6.264384 36.800668
P-H
4
2 11.413867 87.002091
2 10.329215 174.004370
2 5.707424 8.870610
2 4.828165 17.902438
D-H
4
2 7.430963 49.883655
2 8.321990 74.684549
2 4.609642 6.486227
2 3.511507 9.546821
F-H
2
2 3.084639 8.791640
2 3.024743 11.658456
G-H
2
2 3.978442 -5.234337
2 4.011491 -6.738142

>>>>

Step 3: Now you can run the global optimization:

$ isomer au6.inp > au6.out

After the optimization, the end of au6.out is

au6.out

Reordered from low to high energy:
===============================================================
    #          Energy      Match-RMSD
===============================================================
    1   -814.38125305      0.00000000
    3   -814.38117940      1.43811738
    4   -814.38099683      0.02502934
    7   -814.38067642      1.44986858
    0   -814.37928321      0.05173414
   19   -814.32702207      1.02885421

So the global minimum is au6-LM/1.xyz and is shown below: