8.1. For Molecular Clusters: Many-Body Energy Decomposition Analysis

The procedure of doing many-body energy decomposition analysis (MB-EDA) can be found in Example: (H2O)6 and Example: Li+, Na+, and Cs+ in (C6H6)6. Here we will give some theoretical arguments.

8.1.1. TSO-EDA

TSO-EDA is based on target state optimization self-consistent field method (J. Chem. Theory Comput. 2023, 19, 1777) and decomposes the total interaction energy into five terms, i.e. electrostatic, exchange, polarization, charge transfer, and dispersion energies. The sum of electrostattic and exchange energy is the Heitler-London term (Phys. Chem. Chem. Phys. 2024, 26, 17549):

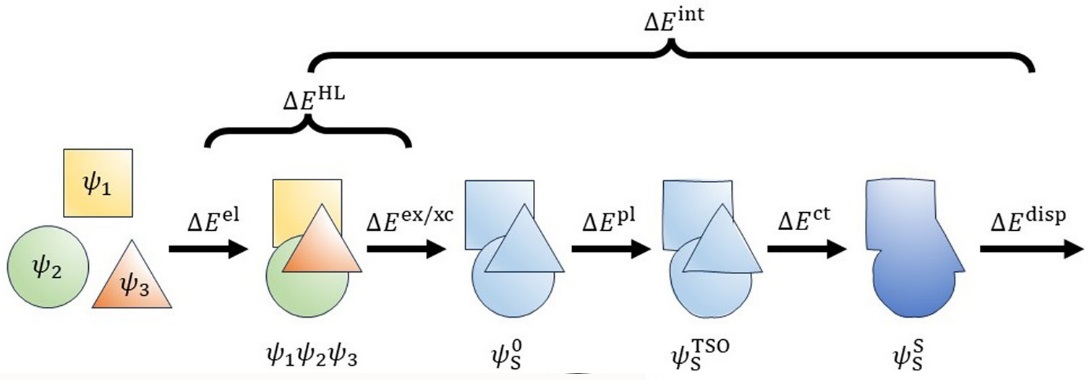
Here:

• Ectrostatic term: Represents the semiclassical Coulombic interaction of charged particles from different monomers;

• Exchange term: Represents quantum effect due to the antisymmetric character of the electronic wave function and the satisfaction of the Pauli exclusion principle;

• Polarization term: Represents the polarization of the electron density of one monomer by the presence of other monomer;

• Charge transfer term: Represents the charge transfer between monomers;

• Dispersion term: Represents the dispersion interaction between monomers.

The BSSE effect is included in charge transfer term. All above terms can be found in Qbics output.

8.1.2. Many-Body TSO-EDA

This method is developed in Phys. Chem. Chem. Phys. 2024, 26, 17549 and is used to analyze the many-body effects in a molecular cluster. The total interaction energy is decomposed into 2-body, 3-body, and higher-order terms, like this:

\[\Delta E^{\text{int}} = \frac{1}{2!} \sum_{I_1 \neq I_2}^{N} \Delta E_{I_1 I_2}^{(2)} +\frac{1}{3!} \sum_{I_1 \neq I_2 \neq I_3}^{N} \Delta E_{I_1 I_2 I_3}^{(3)} + \cdots + \frac{1}{n!} \sum_{I_1 \neq \cdots \neq I_n}^{N} \Delta E_{I_1 \cdots I_n}^{(n)} + \cdots + \Delta E_{I_1 \cdots I_N}^{(N)} \equiv \sum_{n=2}^{N} \Delta E^{(n)}\]

The terms higher than \(\Delta E^{(2)}\) is the many-body interaction term. Usually the most important one is the three-body effect \(\Delta E^{(3)}\), the effects of which can be decomposed into three ones:

• \(\Delta E^{(3)} < 0\): Indicate a cooperative effect of the monomers in a cluster. The many-body interaction is stabilizing the cluster. This is often seen in hydrogen bonding clusters, like water clusters.

• \(\Delta E^{(3)} > 0\): Indicate an anti-cooperative effect of the monomers in a cluster. The many-body interaction is destabilizing the cluster. This is often seen in a cluster of charged species, like ionic liquid clusters. Also see below.

• \(\Delta E^{(3)} \approx 0\): Indicate a non-cooperative effect of the monomers in a cluster. There is little many-body interaction in the cluster. This is often seen in a cluster of molecules without charges or hydrogen bonds.

Each order can be decomposed into electrostatic, exchange, polarization, charge transfer, and dispersion terms:

\[\Delta E_X^{(n)} = \Delta E_X^{(n)\text{-el}} + \Delta E_X^{(n)\text{-ex/xc}} + \Delta E_X^{(n)\text{-pl}} + \Delta E_X^{(n)\text{-ct}} + \Delta E_X^{(n)\text{-disp}}\]

Usually, electrostatic and exchange terms are highly additive, while polarization and charge transfer terms are non-additive. The dispersion term is always additive.

8.1.3. Input Examples

MB-EDA needs to be calculated with Qbics, which can be obtained here: https://zhjun-sci.com/qbics/. The details of compilation can be found here: https://zhjun-sci.com/qbics/doc/compilation.html.

For EDA keyword, please refer to: https://zhjun-sci.com/qbics/doc/keywords/eda.html.

8.1.3.1. Example: EDA for GeH₃F-NCH Complex by B3LYP-D3BJ/def2-SVP

For the complex GeH₃F-NCH, we can do EDA calculation by the following input:

eda-1.inp

mol
   Ge      0.00000000      0.00221863     -0.79935317
    H      0.00000000      1.48645043     -0.40384625
    H      1.28514604     -0.74161126     -0.40477816
    H     -1.28514603     -0.74161126     -0.40477816
    F      0.00000000      0.00108752     -2.56116087
    C      0.00000000     -0.00225138      3.35662076
    H      0.00000000     -0.00220444      4.43604901
    N      0.00000000     -0.00207825      2.20326200
end

basis
    def2-svp
end

scf
    charge  0
    spin2p1 1
    type    U # For EDA calculations, this must be added explicitly.
end

grimmedisp
    type bj
end

eda
    type tso # You can also change it to: gks
    frag 0 1 1-5  # Define GeH3F.
    frag 0 1 6-8  # Define HCN.
end

task
    eda b3lyp
end

The atom indices are shown below:

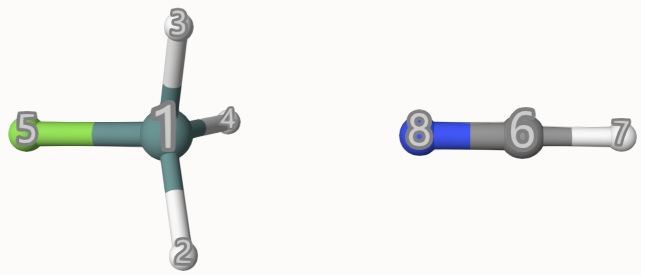
The results are:

eda-tso.out

WITH BSSE correction:
Electrostatic interaction energy:                  -4.98 kcal/mol
Exchange-correlation interaction energy:            4.22 kcal/mol
Polarization interaction energy:                   -0.62 kcal/mol
Charge transfer interaction energy:                -1.31 kcal/mol
Grimme's dispersion interaction:                   -1.58 kcal/mol
----------------------------------------------------------------
Total interaction energy:                          -4.27 kcal/mol

We can see that this complex is stabilized by Electrostatic interaction eneregy, which is compatible with the chemical intuition that it is stabilized by sigma-hole.

8.1.3.2. Example: MB-EDA for Molecular Cluster (NH₄⁺)₂(H₂SO₄)(HSO₄^-)₂

The title cluster is composed of two NH₄⁺ cations, one H₂SO₄ molecules, and two HSO₄^- anions. This cluster is used in the study of atmopheric chemistry.We can do MB-EDA calculation by the following input:

eda-2.inp

basis
    def2-svp
end

scf
    charge     0 # Total charge.
    spin2p1    1
    type       U
end

grimmedisp
    type bj
end

eda
    type      mb_tso
    mb_level  4
    frag  +1 1 1-5   # NH4+
    frag  +1 1 6-10  # NH4+
    frag   0 1 11-17 # H2SO4
    frag  -1 1 18-23 # HSO4-
    frag  -1 1 24-29 # HSO4-
end

mol
 N                  0.13124700   -1.86033100   -1.49054300
 H                 -0.68471400   -1.96085700   -0.84840100
 H                  0.16284500   -2.63375000   -2.14527600
 H                 -0.00155300   -0.97157900   -1.98611500
 H                  1.02982000   -1.79400200   -0.97437700
 N                 -1.89606400    2.02266900    1.95536400
 H                 -2.33766600    1.07911300    1.78190600
 H                 -1.20423600    1.92734800    2.69193100
 H                 -1.40455300    2.34660500    1.08417600
 H                 -2.60508400    2.69280200    2.23215700
 S                  3.40269500   -0.73966700    0.43845300
 O                  4.56636300   -1.26003200    1.03924300
 O                  2.66268100   -1.55477200   -0.49575900
 O                  2.42657400   -0.30120000    1.56959800
 O                  3.78755300    0.58843400   -0.27018200
 H                  2.99297400    1.01172300   -0.68798600
 H                  1.56137200   -0.00498400    1.17228000
 S                 -3.05756300   -0.82805000    0.17173500
 O                 -2.21824200   -1.98280100   -0.09354400
 O                 -3.00471800   -0.39464500    1.56194000
 O                 -2.90973700    0.26502300   -0.77053900
 O                 -4.55472700   -1.30387800   -0.08712900
 H                 -4.73898300   -2.05912100    0.48328300
 H                 -1.51856700    0.72871100   -1.53329100
 S                  0.24159900    1.52238500   -0.65825900
 O                 -0.59336700    0.90131200   -1.85962900
 O                  1.55183900    1.72430300   -1.22252400
 O                 -0.45708500    2.72297400   -0.23978600
 O                  0.20716100    0.49864900    0.39894800
end

task
   eda b3lyp
end

The atom indices are shown below, which is used to define the fragments frag:

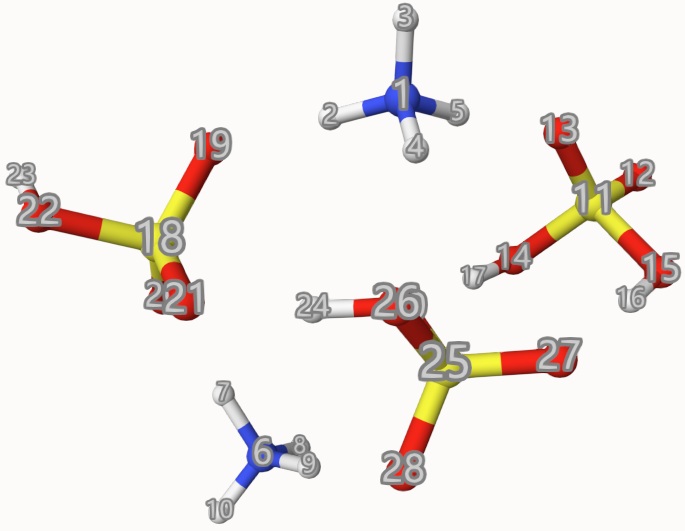
The results are:

eda-2.out

Table 5. Summary (kcal/mol).
---------------------------------------------------------------------------------------------------------------------------------
    Interactions         delE_el         delE_xc         delE_pl         delE_ct       delE_bsse       delE_disp        delE_tot
---------------------------------------------------------------------------------------------------------------------------------
   SUM of 2-body -3.51853640E+02  1.04231044E+02 -5.50310217E+01 -9.70290703E+01  4.35696096E+01 -1.98079059E+01 -3.75920984E+02
   SUM of 3-body  1.72107484E-09  1.45358519E+00  2.82254671E+01  2.81735373E+01 -1.24450163E+01  1.01531078E-02  4.54177264E+01
   SUM of 4-body -4.14670076E-09  1.70212282E-02 -2.25462767E+00 -5.15894065E+00  1.89758583E+00  2.28017787E-05 -5.49893846E+00
          Remain  7.51748885E-09 -8.58522126E-04  6.43113307E-02  4.30266615E-01 -1.22896862E-01  5.97720460E-07  3.70823167E-01
---------------------------------------------------------------------------------------------------------------------------------
             SUM -3.51853640E+02  1.05700792E+02 -2.89958710E+01 -7.35842070E+01  3.28992822E+01 -1.97977294E+01 -3.35631373E+02
---------------------------------------------------------------------------------------------------------------------------------

We can see that the total interaction energy is -335.63 kcal/mol, which is decomposed into 2-body, 3-body, 4-body, and remaining terms. The 2-body term is the most important one (-375.92 kcal/mol), while the 3-body term is also significant, but anti-cooperative (destablizing the complex) (+45.42 kcal/mol). The 4-body term is small (-5.50 kcal/mol, slightly cooperative). The remaining term (sum of 5- and 6-body) is very small (+0.37 kcal/mol) and can be ignored.

We can also see that the electrostatic and exchange energy are highly additive, while the polarization and charge-transfer energy are non-additive. For different kinds of clusters, the 3-body effects (many-body interactions) can be quite different, see Phys. Chem. Chem. Phys. 2024, 26, 17549 for more information.