2. Theoretical Background

ABCluster is a black-box program, meaning that you can do global optimization of clusters without knowing too much about theories behind ABCluster. Of course, it will be beneficial if you understand some basic principles. In this section, some global optimization theories and experiences will be briefly introduced.

2.1. Global Optimization

Tip

If you would like to know more about global optimization, I strongly recommend the following paper:

Clusters with different ways of packing their structural units will obviously have different energies, although sometimes the energy difference can be very small (< 1 kcal mol -1). If a cluster is built by randomly packing structural units, a simple local optimization like using OPT in Gaussian or integrator = cg in Gromacs seldomly leads to a cluster of low energy, because there are many local minima (LMs), or more chemically, isomers, on the potential energy surface (PES) of the cluster. These isomers are separated by a lot of barriers, and local optimization is unable to overcome all barriers. So, this randomly packed cluster may haver very high energy and might not represent the ones occurred in experiments, giving unreasonable or even misleading results in theoretical studies. Therefore, it is critical to look for isomers that have energies as low as possible.

Global optimization intends to solve this problem. In the context of chemical clusters, global optimization is an algorithm to look for the most stable isomer (the cluster having the lowest energy, i.e., global minimum, GM) on the PES by using some ways to escape LM traps. These “ways” determine what a global optimization algorithm is. There are many algorithms, like basin hopping, genetic algorithm and artificial bee colony (ABC) algorithm. The ABC algorithm needs only 3 or less parameters, thus is easy to learn and control. It is the essential part in ABCluster and has been proved to be highly successful!

One must keep in mind that unlike LMs, which can be discriminated by zero coordinate gradients, there is no robust way to discriminate a GM. Thus, the GM predicted by ABCluster (and other programs) can only be treated as a putative one. One must use chemical intuition to question and answer “Is there a more stable cluster?” Otherwise, one can run several global optimizations with different parameters to cross-validate the reliability of GM.

Tip

For the ability of global optimization, these two points are useful:

  • For small clusters (number of structural units < 25), modern global optimization algorithms can usually find the true GM at an acceptable cost. So, you should try hard to find the true GM for systems like \(\mathrm{Cu}_{16}\) or \(\left(\mathrm{N}\mathrm{H}_3\right)_{15}\).

  • For large clusters, no one can guarantee that a “true” GM can be found, but a cluster of very, very low energy can be usually obtained. In many cases, this cluster is sufficient for theoretical studies.

During the global optimization of ABCluster, it will generate not only the GM, but also a lot of LMs. These structures are very important for you to draw a big picture of the whole PES. Indeed, sometimes both the global and some low-lying LMs will contribute to the experimental observations. Thus, do not only look at the GM. LMs can also provide chemical insights into your problem!

Tip

Here is an example. The global optimization of \(\mathrm{Au}_8\) supported on graphene oxide (GO) was done here. In the GM and a LM, some gold atoms form covalent bonds with oxygen atoms on GO. In some other LMs, no covalent bonds form between gold atoms and GO, and \(\mathrm{Au}_8\) that has a geometry similar to the GM of \(\mathrm{Au}_8\) in gas phase is the most stable one in these LMs. Thus, it looks like that there are two classes of gold clusters supported on GO: “GO-corrupted” and “GO-uncorrupted” ones. In GO-uncorrupted clusters, GO has little impact on the stability order of \(\mathrm{Au}_8\) isomers.

2.3. Energy Evaluation

2.3.1. Rule of Thumb

Global optimization intends to find clusters of low energy. So, how to evaluate this energy? There are two factors to be considered:

  • Reliability. The energy must be calculated as accurate as possible to give reliable results. What method is suitable for my system? B3LYP or TPSSh? Semi-empirical methods or force fields? To answer these questions, you need to rely on your (correct) computational chemistry experiences, check the literature or even do method calibrations before global optimization.

  • Cost. High accuracy is expensive. Remember this computational time cost:

Method

Cost

Force fields

1

Semi-empirical methods

1,000

ab initio methods (gas phase)

10,000~100,000

ab initio methods (periodic systems)

300,000~1,000,000

Note that, it is routine to carry out 500~10,000 or more geometry optimizations to do a reliable global optimization. Therefore, a compromise between reliability and cost must be made.

Here I give a rule of thumb: always use cheaper but reliable methods to do the first exploration, and then use high-level methods to refine the results! Below is a typical scheme.

Tip

In atmospheric chemistry, researchers are interested in some molecular clusters. Obtaining reliable GMs requires accurate calculation of energies. This paper proposed a systematic way to achieve this:

  1. Do global optimization of molecular clusters with ABCluster at CHARMM force field level of theory and finally get 10,000 LMs.

  2. These 10,000 LMs are optimized at GFN-xTB level of theory. After discarding about 9,000 high-energy clusters, about 1,000 ones are remained.

  3. The 1,000 clusters are optimzed at wB97XD/6-31++G(d,p) level of theory with loose convergence criteria. Select some low energy ones and re-optimized them with tight convergence criteria.

  4. 10 energetically lowest-lying clusters are then sent to DLPNO-CCSD(T)/aug-cc-pVTZ calculations to determine the most accurate energies.

The scheme above is very reasonable, and in practice you can modify this to adapt to your own systems.

Below, I will give some general rules about the selection of energy evaluation methods.

2.3.2. When does CHARMM Force Field Perform Well?

Clusters containing ordinary organic and closed-shell inorganic species can be described quite well by CHARMM force field. Thus, one can use rigidmol. In such cases, using expensive quantum chemistry method at the beginning is unnecessary. However, as mentioned above, the obtained low energy clusters must be further optimized and studied using ab initio methods.

2.3.3. When Must Quantum Chemistry Method be Used?

Generally, clusters with delocalized electronic structures should be described using quantum chemistry methods at the beginning. Here, “quantum chemistry methods” can be semi-empirical ones like GFN2-xTB or ab initio ones like DFT.

  • Atomic clusters, like \(\mathrm{Au}_{20}\), \(\mathrm{B}_{8}\mathrm{N}_{8}\).

  • Inorganic clusters, like \(\mathrm{Co}_6\mathrm{Te}_8\left(\mathrm{PEt}_3\right)_6\).

  • Clusters with extra, absent electrons or special spin multiplicities, say \(\left(\mathrm{H}_2\mathrm{O}\right)_{10}^{-}\). Note that “extra, absent electrons” should be understood correctly. For example, sodium cation is a closed-shell species that can be described quite well by CHARMM force field, but sodium atom must be treated quantum chemically.

  • Periodic systems, like surface-supported clusters. In these cases, one should connect ABCluster with CP2K, VASP, etc.

2.3.4. Be Cautious with Model Potentials!

In atom, there are several model potentials that have been developed for different purposes. These potentials cannot be simply recognized as approximations of ab initio theory. Actually, they are preferred by physicists. When applied to chemical problems, you must exactly know what you are doing and be cautious in interpreting the global optimization results!

Attention

For example, Gupta potential is very popular for describing metallic clusters. However, these ones are usually fitted with condensed phase properties and may be a bad choice for small clusters. Say \(\mathrm{Au}_{20}\), one can obtain a tetrahedral GM using DFT which can interpret experimental observations. However, Gupta potential will give an irregular polyhedral GM, which is obviously a misleading result. But, if you immediately need a good initial structure guess of large clusters like \(\mathrm{Au}_{80}\), Gupta potential will be a good choice.

2.4. The Artificial Bee Colony Algorithm

Tip

For more details, please refer to:

The ABC algorithm was proposed by Karaboga in 2005. The ABC algorithm mimics the foraging behavior of bees. Three kinds of bees are distinguished in a colony: employed bees (EM), onlooker bees (OL) and scout bees (SC). A colony tries to find the best nectar as food source. To do this, EMs perform an trail search; OLs based on the knowledge of all EMs perform a further research; SCs search completely new areas. After several cycles of search, the colony can find the best nectar.

This scheme has been transferred to ABCluster. The basic flowchart of a global optimization is:

  1. Set \(g = 0\);

  2. A total number of \(SN\) cluster structures (population) are randomly generated;

  3. In generation \(g\), three kinds of operators: EM, OL, and SC, are applied to the population in turn to generate new clusters;

  4. The generated new cluster structures are optimized using the assigned energy evaluation method;

  5. Update the population using the optimized new cluster structures.

  6. If \(g \ge g_\mathrm{max}\), the global optimization terminates; otherwise set \(g = g+1\) and go back to Step 3.

A typical ABC global optimization needs three parameters: the population size \(SN\), the maximum of search generation \(g_{\mathrm{max}}\), and the scout limit \(g_{\mathrm{limit}}\) (for SC operators). Sometimes, an estimate of the cluster length \(L\) is also required.

Below is a typical choice of these parameters for atom and rigidmol:

Parameter

Value

\(SN\)

10~300

\(g_{\mathrm{max}}\)

100~100,000

\(g_{\mathrm{limit}}\)

3~5

\(L\)

1.5 to 3 times larger than the system size

For isomer and geom, only \(g_{\mathrm{max}}\) is needed. Usually it should be larger than 500. Modern applications of global optimization on large systems may need a value larger than 20000.

Tip

  • For clusters dominated by long-ranged interactions such as Coulombic ones, the global optimization is relatively easier, like \(\mathrm{K}^{+}\left(\mathrm{H}_2\mathrm{O}\right)_{20}\), where the dominating interactions are the charge-dipole ones between the potassium cation and water moelcules. For clusters dominated by short-ranged interactions such as dispersion, covalent bonds, and hydrogen bonds, the global optimization is usually more difficult, so \(SN\) and especially \(g_{\mathrm{max}}\) should be large to get reliable GMs. This is a result of the topology of PES. See this review for details.

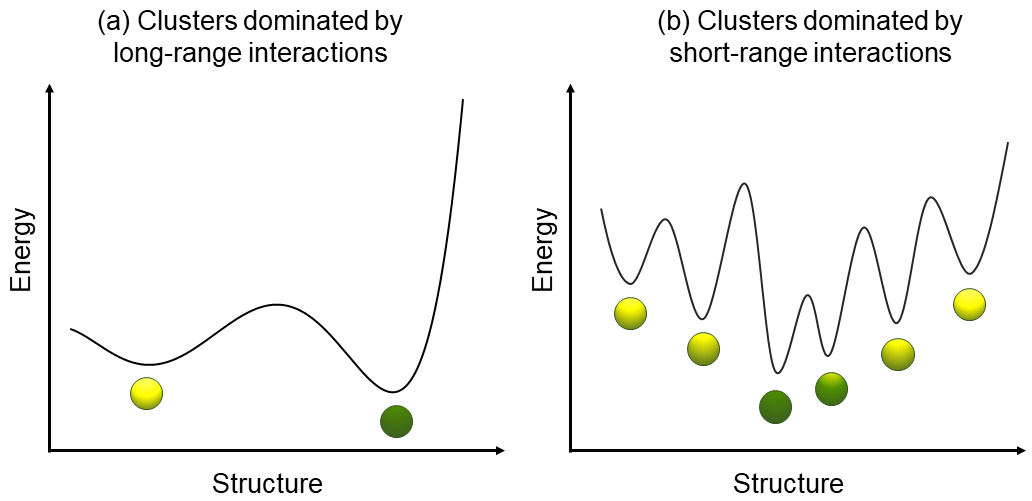
alternate text

  • For difficult cases (large clusters), one can run several global optimizations simultaneously for cross validation.

2.5. Automatic Atom Typing

Tip

The details of this part is here:

For organic molecules, it is beneficial to use CHARMM force field to do global optimization, since it is much faster than quantum chemistry. However, a big barrier is to assign atom types to all atoms that are consistent with CHARMM force field. In old versions, such atom typing, i.e., building parameter files, has to be done manually, which is a boring work. From ABCluster 3.1, graph representation learning (technically, topology adaptive graph convolution networks, TAGCNs) has been successfully applied to this job automatically. In many cases, it can generate highly reliable typing. Briefly, the basic principle behind this is that several TAGCNs were trained using more than 700 typed molecules. TAGCNs “learned” chemistry during this training process and “remembered” rules as some sort of distributions of weights. This process is transparent to the users of ABCluster: one just gives coordinates and ABCluster will do everything for atom typing.