3.7. Example: C16 and Ge16
Tip
The sample input and output files can be found in testfiles/atom/5-cge.
\(\mathrm{C}_{16}\) and \(\mathrm{Ge}_{16}\) are inorganic clusters with very delocalized electronic structures. In principle, one should use DFT to carry out global optimization. However, one can use Tersoff potential to do a first exploration. The parameters can be found in misc/atomic-force-field.txt:
C-C 1393.6 346.7 3.4879 2.2119 0.0000001524 0.72751 38049.0 4.384 -0.57058 1.8 2.1 1.0 1.0 # Phys. Rev. B 1989, 39, 5566
Si-Si 1830.8 471.18 2.4799 1.7322 0.0000011 0.78734 100390 16.217 -0.59825 2.7 3.0 1.0 1.0 # Phys. Rev. B 1988, 38, 9902
This suggests that these parameters are taken from the paper J. Phys. C 1985, 18, 1149. The parameters are ordered exactly the one that abcinp needs. Just simply copy them to abcinp.
For \(\mathrm{C}_{16}\):
Step 1: call abcinp to generate input files:
abcinp c16 1 Tersoff 8 50 10000 5 10 16 C
Parameters for atom 0: A B lambda mu beta m c d h R S > 1393.6 346.7 3.4879 2.2119 0.0000001524 0.72751 38049.0 4.384 -0.57058 1.8 2.1
Parameters for atom-pair 0-0: kai omega > 1.0 1.0
Tip
You may find that the population size and maximum cycle number are very large. The reason is that, as mentioned in Theoretical Background, Tersoff potential is rather short-range (valence dependence), which is difficult for global optimization.
Step 2: Run the global optimization:
$ atom c16.inp > c16.out
After a few seconds, you will find the global minimum in c16.xyz and local minima in c16-LM.
For \(\mathrm{Ge}_{16}\), the global optimization is similar.
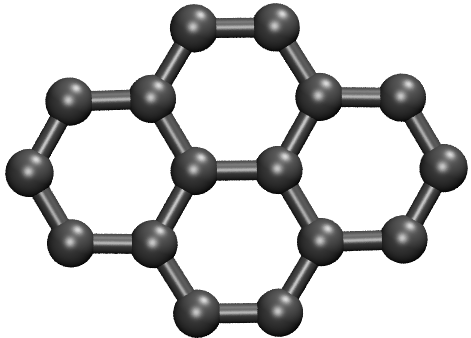
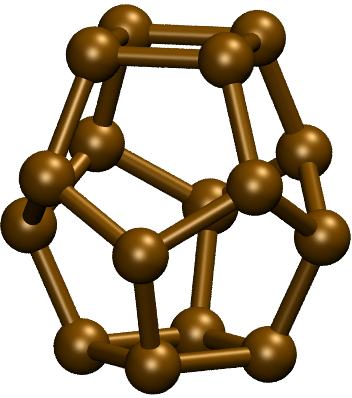
The global minima of \(\mathrm{C}_{16}\) and \(\mathrm{Ge}_{16}\) are shown below. They seem to be quite reasonable.