6.4. geom with Gaussian
Tip
Gaussian is suitable for any clusters in gas phase, as long as you choose the correct model (pure, hybrid, or double-hybrid DFT, CCSD(T), and basis sets), but it is also expensive. So, this should only be used when there is no better ways.
In this Section, we just want to demonstrate how to use Gaussian with geom. Actually, it is possible that xTB is used first to get reliable structures, then Gaussian is used to refine, as discussed in Theoretical Background.
6.4.1. Example: (H2O)4-
Tip
The sample input and output files can be found in testfiles/geom/2-h2o4e-g16.
In this Section we will see how to use geom and Gaussian to do global optimization. Actually, this is exactly the same as we do in isomer with Gaussian: you just need to copy the commands to commands block.
The cluster we consider here is \(\left(\text{H}_2\text{O}\right)_4^{-}\), an electron solvated in 4 water molecules. We will use the following input:
1lm_dir h2o4e # Save the local minima to this folder.
2num_calcs 50 # Total number of calculations.
3do_coarse_opt yes # no: Do NOT the coarse optimization.
4min_energy_gap 1.E-4 # When two energies differ smaller than
5 # this value, they are treated as identical.
6 # A negative number means do not remove
7 # energetically degenerated ones.
8max_geom_iters 3000 # The maximum number of iterations for local optimization.
9 # If it is less or equal than zero, then the number is unlimited.
10
11components
12 h2o.xyz 4
13 random 0 0 0 6 6 6
14 ****
15end
16
17savegjf
18 %chk=h2o4-$index$.chk
19 %nproc=48
20 %mem=30GB
21 $hash$MP2/aug-cc-pVTZ Opt Freq Output=wfn
22 $blank$
23 Initial guess generated from ABCluster, energy = $energy$
24 $blank$
25 -1 2
26 >>>>
27 h2o6-$index$.wfn
28end
29
30commands
31 xyz2gaussian optfile $inp$ > $xxx$.gjf
32 g16 < $xxx$.gjf > $xxx$.log 2>/dev/null
33 gaussian2xyz $xxx$.log > $out$
34end
You can see that, the commands to call Gaussian in commands is the same to the ones in isomer with Gaussian. We will calculate 50 structures and save them to heo4e. We also add a savegjf block to let geom save LMs in Gaussian job input format.
Also, we use random instead of box because we hope to get more flexible initial guess for global optimization.
The structure of \(\text{H}_2\text{O}\) is:
13
2water
3O 0.00000000 0.00000000 -0.11081188
4H 0.00000000 -0.78397589 0.44324751
5H -0.00000000 0.78397589 0.44324751
The Gaussian input template is:
1%nprocs=48
2%mem=20GB
3%chk=h2o4e.chk
4#N B3LYP/6-31++g(d) SCF(XQC) Geom(NoCrowd) Opt
5
6opt
7
8-1 2
9>>>>
10>>>>
Now you can run the global optimization:
$ geom h2o4e.inp > h2o4e.out
After the optimization, the end of h2o4e.out is
-- Result Report --
Results are energy-increasingly reordered.
Structures of energies within 1.000E-04 are treated as degenerate.
All minima are saved to "h2o4e".
-------------------------------------------------------------------
# index Energy NaiveRMSD
-------------------------------------------------------------------
0 32 -305.73627036 0.00000000
1 8 -305.73593799 1.92341824
2 1 -305.73517045 1.95589313
3 47 -305.73433736 2.14224379
4 16 -305.73402914 1.52860669
5 33 -305.73371713 1.31278433
6 34 -305.73312443 0.94350149
7 25 -305.73243751 1.49950503
8 23 -305.73225990 1.78428545
9 38 -305.73083814 2.34486039
10 29 -305.73055667 1.64935620
So the global minimum is h2o4e/32.xyz, which is shown below. Interestingly, the anionic cluster optimized starting with the GM of neutral \(\left(\text{H}_2\text{O}\right)_4\) is higher in energy than h2o4e/32.xyz by 1.37 kcal/mol at B3LYP/6-31g++(d).

Tip
We use B3LYP/6-31++g(d) to study the system. However, since the addition electron in this system may be very delocalized, very diffuse basis functions and high level of theory (beyond MP2) are needed to get reasonable results. That is why we let geom to generate GJF files for LMs. You can run more accurate calculations for the top 5 or 10 LMs to further refine the true GM.
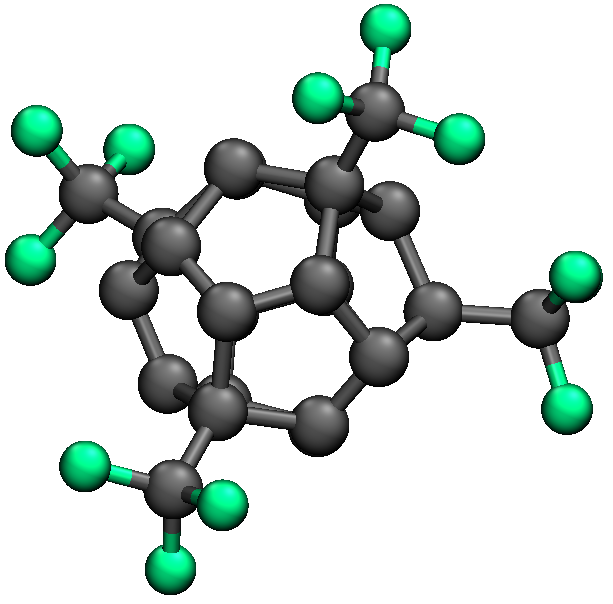
6.4.2. Example: (CF3)4@C20
Tip
The sample input and output files can be found in testfiles/geom/3-c20cf34-g16.
It is argued that carbon cage like \(\text{C}_{20}\) is an electron acceptor. So what will happen if some electron-withdrawing groups are attached? Let’s try to build a cluster of 4 \(\text{-CF}_3\) on \(\text{C}_{20}\).
The structures of \(\text{C}_{20}\) and \(\text{-CF}_{3}\) are:
120
2C20
3C -1.20472114 0.39143763 1.65815580
4C -0.74455861 -1.02479702 1.65815580
5C 1.20472114 0.39143763 1.65815580
6C -0.00000000 1.26671877 1.65815580
7C 0.00000065 2.04959354 0.39143762
8C -1.20471985 1.65815687 -0.39143704
9C 1.20472125 1.65815590 -0.39143685
10C 0.74456049 1.02479624 -1.65815544
11C -0.74455796 1.02479756 -1.65815575
12C 1.20472204 -0.39143886 -1.65815486
13C 1.94927928 -0.63336012 -0.39143623
14C 1.94927917 0.63335933 0.39143808
15C 0.74455861 -1.02479702 1.65815580
16C 1.20472070 -1.65815601 0.39143808
17C 0.00000038 -2.04959369 -0.39143685
18C -1.20472033 -1.65815639 0.39143762
19C -1.94927899 -0.63336053 -0.39143704
20C -1.20472093 -0.39143845 -1.65815575
21C 0.00000048 -1.26672037 -1.65815458
22C -1.94927868 0.63336060 0.39143848
14
2CF3
3C 0.00000000 0.00000000 -0.36818188
4F -1.10227044 -0.63639614 0.08181821
5F 0.00000000 1.27279228 0.08181821
6F 1.10227044 -0.63639614 0.08181821
The input file is:
1lm_dir c20cf34 # Save the local minima to this folder.
2num_calcs 5 # Total number of calculations.
3do_coarse_opt yes # no: Do NOT the coarse optimization.
4min_energy_gap 1.E-4 # When two energies differ smaller than
5 # this value, they are treated as identical.
6 # A negative number means do not remove
7 # energetically degenerated ones.
8max_geom_iters 3000 # The maximum number of iterations for local optimization.
9 # If it is less or equal than zero, then the number is unlimited.
10
11components
12 c20.xyz 1
13 fix 0 0 0 0 0 0
14 ****
15 cf3.xyz 4
16 shell 1 1 1 2 3 4 0 0 0 3 3 3
17 ****
18end
19
20commands
21 xyz2gaussian optfile $inp$ > $xxx$.gjf
22 g16 < $xxx$.gjf > $xxx$.log 2>/dev/null
23 gaussian2xyz $xxx$.log > $out$
24end
From components, we can see that \(\text{C}_{20}\) is fixed at (0, 0, 0) without rotation. Since its diameter is about 6 Å, we let the 4 \(\text{-CF}_{3}\) groups form a shell on an ellipsoid centered at (0, 0, 0) with radii 3, 3, and 3. They point to the shell with an axis defined by the average of atom 1, 1, 1 and 2, 3, 4. This system is very expensive, so we do only 5 calculations.
The Gaussian template is:
1%nprocs=48
2%mem=20GB
3%chk=c20cf34.chk
4#N wB97XD/gen Opt
5
6opt
7
80 1
9>>>>
1021 25 29 33
116-31g(d)
12****
13F 0
146-31g(d)
15****
161 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
173-21g
18****
19>>>>
Here, we choose wB97XD instead of B3LYP because the latter usually performs poorly for aromatic systems. After the first >>>>, we define the basis sets for different atoms to save the computational cost
Tip
This basis set canNOT be used in real scientific research. A better one is def2-SVP. For property calculations, triple-zeta and diffusion functions may be required.
Now you can run the global optimization:
$ geom c20cf34.inp > c20cf34.out
After the optimization, the end of c20cf34.out is
-- Result Report --
Results are energy-increasingly reordered.
Structures of energies within 1.000E-04 are treated as degenerate.
All minima are saved to "c20cf34".
-------------------------------------------------------------------
# index Energy NaiveRMSD
-------------------------------------------------------------------
0 2 -2107.38065472 0.00000000
1 0 -2107.38019685 1.83056800
2 1 -2107.37839045 3.12425180
3 3 -2107.37619597 3.38430408
4 4 -2106.56831104 2.73267963
-------------------------------------------------------------------
So the global minimum is c20cf34/2.xyz, which is shown below.